三次元姿勢表現方法
回転行列
回転行列は最も基礎的な三次元回転表現方法で、3×3の直交行列により座標系間の回転関係を記述します。回転行列は厳密な数学的性質を有します:行列の行列式は1であり、行列の逆行列はその転置と等しくなります。回転行列は数学的には非常に厳密ですが、実際の応用においていくつかの課題が存在します。
回転行列は3つの自由度の回転を記述するのに9つのパラメータを必要とし、冗長性が存在します。同時に、回転行列による回転記述は非常に直感的でなく、その幾何学的意味を直接理解することが困難です。したがって、実際のエンジニアリング応用では、通常他のより直感的でコンパクトな表現方法が必要となります。
オイラー角
オイラー角は比較的直感的な姿勢表現方法を提供し、複雑な三次元回転を異なる軸の周りの3回の回転に分解します。分解方式が複数あるため、オイラー角にも異なる定義方法が存在し、大まかに2つのカテゴリに分けられます:固定軸周りの回転(固定角とも呼ばれる)と回転後の軸周りの回転です。
RPYオイラー角システム
比較的よく使用されるオイラー角の一つがRPY(「ヨー・ピッチ・ロール」/Yaw-Pitch-Roll)で、ZYX軸の回転と等価です:
-
物体のZ軸周りに回転し、ヨー角Yawを得る
-
回転後のY軸周りに回転し、ピッチ角Pitchを得る
-
回転後のX軸周りに回転し、ロール角Rollを得る
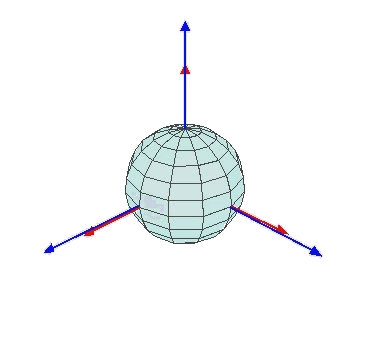
この表現方法は航空宇宙およびロボット学で広く採用されており、物体運動に対する人々の直感的理解に適合しているためです。ヨー角は物体の左右方向制御、ピッチ角は上下傾斜制御、ロール角は側方回転制御を行います。

ジンバルロック問題
オイラー角は比較的直感的ですが、ジンバルロック(Gimbal Lock)と呼ばれる問題が存在します。ピッチ角が正負90度の時、第1回転と第3回転が同一軸を使用することになり、システムが1つの自由度を失い、特異性が発生します。したがって、オイラー角は補間や反復には適しません。
ジンバルロックの発生過程は以下の画像シーケンスで理解できます:

正常な状況下では、ヨー角はZ軸周りの回転を独立して制御でき、3つの回転軸は相互に独立しています。

ピッチ角が正常範囲内にある時、3つの回転軸は依然として独立性を保持し、完全な三次元回転を実現できます。
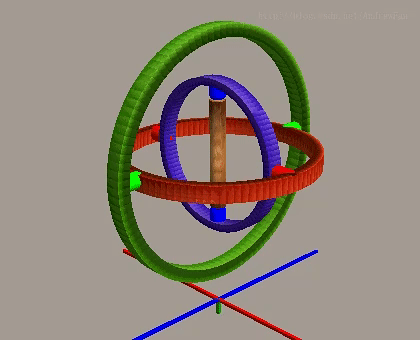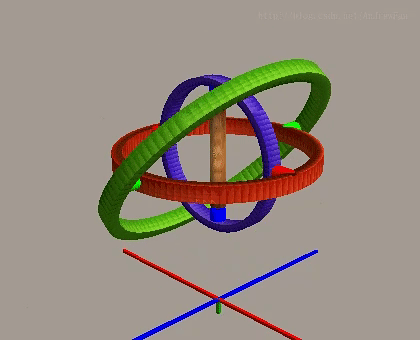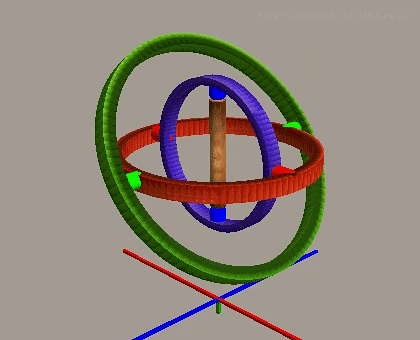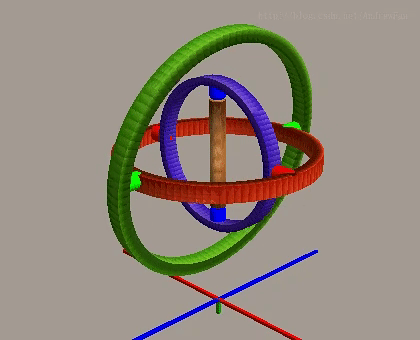
ロール角は正常状況下でX軸周りの回転を制御し、他の2つの軸と相互に独立しています。

しかし、ピッチ角が±90度に達すると、第1回転軸(ヨー軸)と第3回転軸(ロール軸)が共線または平行になり、システムは1つの回転自由度を失い、2つの自由度の回転のみ実現可能となります。この現象をジンバルロックと呼び、オイラー角表現法の固有の限界です。
|
ジンバルロックは理論的問題だけでなく、実際のロボット制御において、ロボット末端エフェクタが特異姿勢に近づく時、突然の大幅回転や運動不連続現象が現れる可能性があり、これは精密操作では受け入れられません。 |
クォータニオン
クォータニオンは非常に効果的な三次元回転表現方法で、オイラー角の特異性問題を克服でき、q = w + xi + yj + zkと記述できます。ここでw、x、y、zはすべて実数成分です。回転として使用する場合、クォータニオンは「単位ノルム」を満たす必要があり、すなわちw² + x² + y² + z² = 1です。
利点:
-
オイラー角のような「ジンバルロック」問題を回避でき、特異点がなく、任意の三次元姿勢の記述に適しています。
-
複数の回転を複合する時、クォータニオン乗法のみを行えばよく、効率が高く、数値的に安定しています。
-
回転補間計算に適しています。球面線形補間(SLERP)により2つのクォータニオン間で滑らかな回転経路を生成でき、これはロボット軌跡計画で非常に有用です。
欠点:
-
クォータニオンと実際の三次元回転間の関係は直感的な幾何学で理解することが容易でなく、理解の敷居が高いです。
-
コンピュータでクォータニオンを用いて変換を繰り返し行う時、数値誤差によりクォータニオンが単位クォータニオンでなくなりやすく、定期的な正規化が必要です。
-
クォータニオンには表現冗長性も存在し、qと-qは同一回転を表すため、特定のアルゴリズムで困惑を生じる可能性があり、特別な処理が必要です。
回転ベクトル
回転ベクトルはRodrigues回転公式に基づく別の簡潔な三次元回転表現方法を提供します。任意の三次元回転は「ある方向周りにどの程度回転するか」として理解できます。例えば「x軸周りに30度回転」、「[1,1,0]方向周りに45度回転」などです。この「方向」を三次元ベクトル(例えば[1,0,0]はx軸方向を表す)で表し、「回転角度」を数値で表します。両者を乗算したものが回転ベクトルです。
利点:
-
回転ベクトル表現方式は簡潔で、小角度回転の記述に適しています。
-
回転行列との相互変換が容易です。
欠点:
-
回転角度が180度に近づく時、回転ベクトルの数値が不安定になり、微小な変化が回転結果の大きな変化を引き起こす可能性があり、実装時に特別な注意が必要です。
-
オイラー角のような直感性もなく、クォータニオンのような数値的堅牢性もありません。
剛体変換
ロボット学において、姿勢(回転)の記述だけでは往々にして不十分で、位置(平移)の同時記述も必要です。剛体変換はまさにこの問題を解決するために提案された統一表現方法です。
剛体変換は物体の三次元空間における回転と移動(平移)を指しますが、物体の形状と大きさは変化させません。通常4×4の同次行列で表現されます:
[ R T ]
[ 0 1 ]ここでRは3×3の回転行列、Tは3×1の平移ベクトルです。この4×4行列は一つの座標系の別の座標系に対する位置と姿勢関係を完全に記述します。
同次座標の導入により、回転と平移を統一して行列乗法で表現できます。空間内の点Pに対し、新座標系におけるその座標P’は簡単な行列乗法により得られます:P' = T × P、ここでPとP’はともに同次座標で表現されます。
利点:
-
物体の空間における位置と方向を完全に記述でき、空間運動の統一表現に適しています。
-
行列乗法による多次変換の組み合わせを直接サポートし、ロボット運動学、図形変換などに適用できます。
-
剛体変換行列は良好な数値安定性も有し、連続的な変換操作により過大な誤差が累積されることはありません。
|