三维姿态表示方法
旋转矩阵
旋转矩阵是最基础的三维旋转表示方法,它通过3×3的正交矩阵来描述坐标系之间的旋转关系。旋转矩阵具有严格的数学性质:矩阵的行列式为1,且矩阵的逆等于其转置。尽管旋转矩阵在数学上非常严谨,但在实际应用中存在一些问题。
旋转矩阵需要9个参数来描述3个自由度的旋转,存在冗余性。同时,旋转矩阵描述旋转时非常不直观,难以直接理解其几何含义。因此,在实际工程应用中,通常需要其他更直观或更紧凑的表示方法。
欧拉角
欧拉角提供了一种比较直观的姿态表示方法,它将复杂的三维旋转分解成3次绕不同轴的旋转。由于分解方式有多种,欧拉角也存在不同的定义方法,大致可分为两类:绕固定轴旋转(又被称为固定角)和绕旋转之后的轴旋转。
RPY欧拉角系统
比较常用的一种欧拉角为RPY("偏航-俯仰-翻转"/Yaw-Pitch-Roll),等价于ZYX轴的旋转:
-
绕物体的Z轴旋转,得到偏航角Yaw
-
绕旋转后的Y轴旋转,得到俯仰角Pitch
-
绕旋转后的X轴旋转,得到翻转角Roll
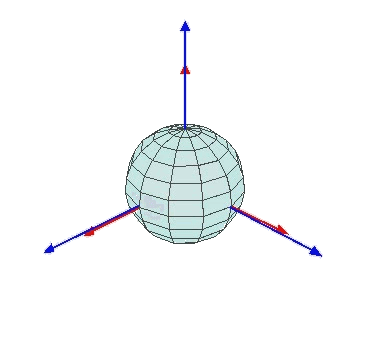
这种表示方法在航空航天和机器人学中被广泛采用,因为它与人们对物体运动的直观理解相符。偏航角控制物体左右转向,俯仰角控制上下倾斜,翻转角控制侧向旋转。

万向节死锁问题
欧拉角虽然比较直观,但存在万向节死锁(Gimbal Lock)问题。在俯仰角为正负90度时,第一次旋转和第三次旋转将使用一个轴,使得系统丢失一个自由度,会发生奇异。因此,欧拉角不适于插值和迭代。
万向节死锁的发生过程可以通过以下图像序列来理解:

在正常情况下,偏航角可以独立控制绕Z轴的旋转,三个旋转轴相互独立。

当俯仰角在正常范围内时,三个旋转轴仍然保持独立性,可以实现完整的三维旋转。
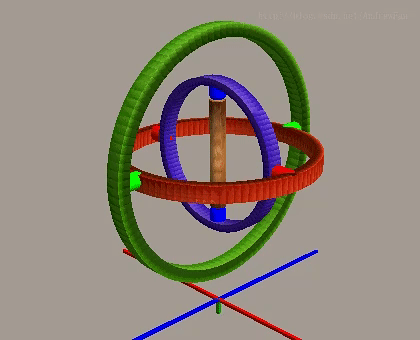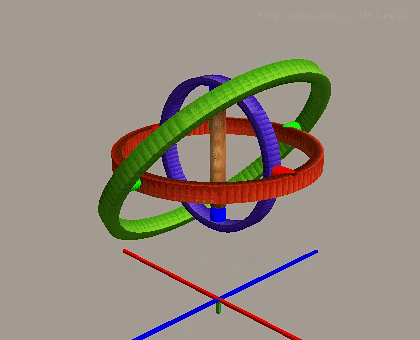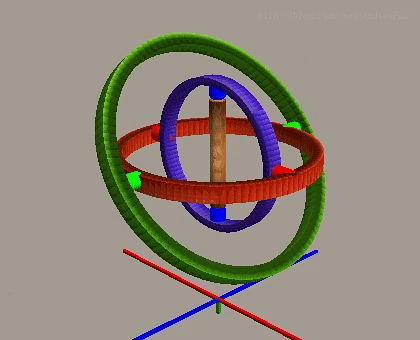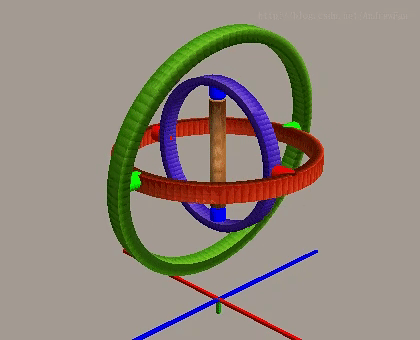
翻转角在正常情况下控制绕X轴的旋转,与其他两个轴相互独立。

但是当俯仰角达到±90度时,第一个旋转轴(偏航轴)和第三个旋转轴(翻转轴)变为共线或平行,系统失去一个旋转自由度,只能实现两个自由度的旋转。这种现象被称为万向节死锁,是欧拉角表示法的固有局限性。
|
万向节死锁不仅是一个理论问题,在实际机器人控制中,当机器人末端执行器接近奇异姿态时,可能出现突然的大幅旋转或运动不连续现象,这在精密操作中是不可接受的。 |
四元数
四元数是一种非常有效的三维旋转表示方法,它能够克服欧拉角的奇异性问题,可以写成q = w + xi + yj + zk,其中w、x、y、z都是实数分量。用作旋转时,四元数需要满足"单位范数",即w² + x² + y² + z² = 1。
优点:
-
可以避免欧拉角那种"万向节死锁"的问题,没有奇异点,适合描述任意三维姿态。
-
复合多个旋转时,只需要做四元数乘法,效率高,数值稳定。
-
适合于旋转插值计算。球面线性插值(SLERP)可以在两个四元数之间生成平滑的旋转路径,这在机器人轨迹规划中非常有用。
缺点:
-
四元数和实际三维旋转之间的关系不容易用直观几何去理解,理解门槛较高。
-
在计算机中反复用四元数做变换时,容易因为数值误差导致四元数不再是单位四元数,需要定期归一化。
-
四元数还存在表示冗余性,q和-q表示同一个旋转,这在某些算法中可能造成困扰,需要特别处理。
旋转矢量
旋转矢量提供了另一种简洁的三维旋转表示方法,它基于Rodrigues旋转公式。任何三维旋转都可以理解为"绕某个方向转多少度"。比如"绕x轴旋转30度","绕[1,1,0]方向旋转45度"。这个"方向"用一个三维向量(比如[1,0,0]表示x轴方向)表示,"旋转角度"用一个数表示。两者相乘,就是旋转矢量。
优点:
-
旋转矢量表达方式简洁,适合描述小角度的旋转。
-
很容易和旋转矩阵互相转换。
缺点:
-
当旋转角度接近180度时,旋转矢量的数值会变得不稳定,微小的变化可能导致旋转结果发生很大变化,需要在实现时特别注意。
-
不像欧拉角那样直观,也没有四元数那样数值鲁棒。
刚体变换
在机器人学中,仅仅描述姿态(旋转)往往是不够的,还需要同时描述位置(平移)。刚体变换正是为了解决这个问题而提出的统一表示方法。
刚体变换指的是一个物体在三维空间中的旋转和移动(平移),但不改变物体的形状和大小。通常用一个4×4的齐次矩阵来表达:
[ R T ]
[ 0 1 ]其中R是3×3的旋转矩阵,T是3×1的平移向量。这个4×4矩阵完整地描述了一个坐标系相对于另一个坐标系的位置和姿态关系。
齐次坐标的引入使得旋转和平移可以统一用矩阵乘法来表示。对于空间中的一个点P,其在新坐标系中的坐标P’可以通过简单的矩阵乘法得到:P' = T × P,其中P和P’都用齐次坐标表示。
优点:
-
能完整描述物体在空间中的位置和朝向,适合做空间运动的统一表示。
-
支持直接用矩阵乘法进行多次变换的组合,适合用于机器人运动学、图形变换等。
-
刚体变换矩阵还具有良好的数值稳定性,不会因为连续的变换操作而累积过大的误差。
|