3차원 자세 표현법
회전 매트릭스
회전 매트릭스는 가장 기본적인 3차원 회전 표현 방법으로, 3×3 직교 행렬을 통해 좌표계 간의 회전 관계를 설명합니다. 회전 매트릭스는 엄격한 수학적 성질을 가지고 있습니다: 행렬의 행렬식이 1이며, 행렬의 역행렬이 그 전치행렬과 같습니다. 회전 매트릭스가 수학적으로 매우 엄밀하지만, 실제 응용에서는 몇 가지 문제가 있습니다.
회전 매트릭스는 3개의 자유도 회전을 설명하기 위해 9개의 매개변수가 필요하여 중복성이 있습니다. 동시에 회전 매트릭스로 회전을 설명할 때 매우 직관적이지 않아 그 기하학적 의미를 직접 이해하기 어렵습니다. 따라서 실제 공학 응용에서는 보통 다른 더 직관적이거나 더 간결한 표현 방법이 필요합니다.
오일러 각
오일러 각은 비교적 직관적인 자세 표현 방법을 제공하며, 복잡한 3차원 회전을 서로 다른 축에 대한 3번의 회전으로 분해합니다. 분해 방식이 여러 가지이므로 오일러 각도 다양한 정의 방법이 존재하며, 대략 두 가지 유형으로 나눌 수 있습니다: 고정축 회전(고정각이라고도 함)과 회전 후 축에 대한 회전입니다.
RPY 오일러 각 시스템
비교적 자주 사용되는 오일러 각 중 하나는 RPY("요-피치-롤"/Yaw-Pitch-Roll)로, ZYX축 회전과 동등합니다:
-
물체의 Z축을 중심으로 회전하여 요 각도(Yaw) 획득
-
회전 후 Y축을 중심으로 회전하여 피치 각도(Pitch) 획득
-
회전 후 X축을 중심으로 회전하여 롤 각도(Roll) 획득
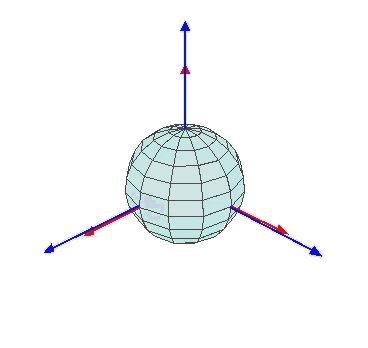
이러한 표현 방법은 항공우주 및 로봇공학에서 널리 채택되는데, 이는 사람들의 물체 운동에 대한 직관적 이해와 부합하기 때문입니다. 요 각도는 물체의 좌우 회전을 제어하고, 피치 각도는 상하 기울임을 제어하며, 롤 각도는 측면 회전을 제어합니다.

김벌 락 문제
오일러 각은 비교적 직관적이지만 김벌 락(Gimbal Lock) 문제가 있습니다. 피치 각도가 양수 또는 음수 90도일 때, 첫 번째 회전과 세 번째 회전이 하나의 축을 사용하게 되어 시스템이 하나의 자유도를 잃고 특이점이 발생합니다. 따라서 오일러 각은 보간과 반복에 적합하지 않습니다.
김벌 락의 발생 과정은 다음 이미지 시퀀스를 통해 이해할 수 있습니다:

정상적인 상황에서 요 각도는 Z축을 중심으로 한 회전을 독립적으로 제어할 수 있으며, 세 개의 회전축이 서로 독립적입니다.

피치 각도가 정상 범위에 있을 때, 세 개의 회전축은 여전히 독립성을 유지하며 완전한 3차원 회전을 실현할 수 있습니다.
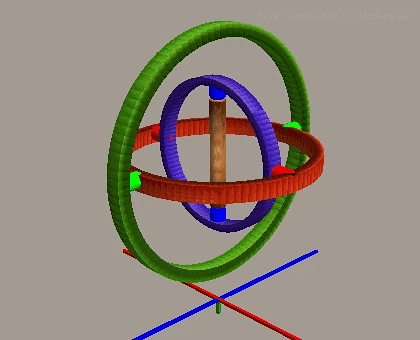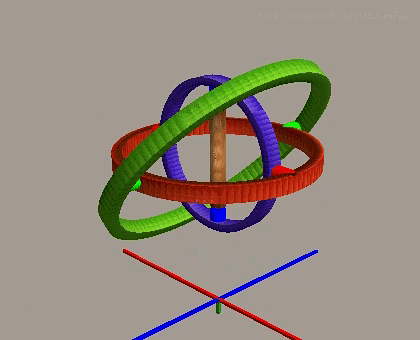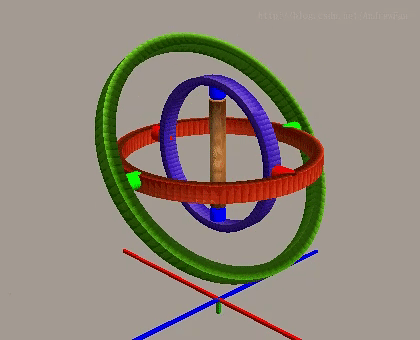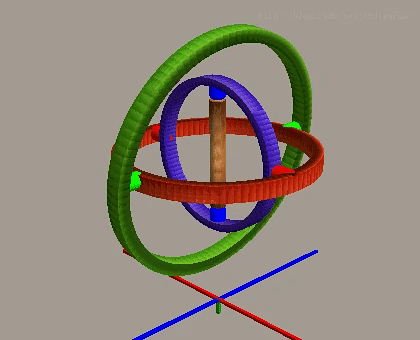
롤 각도는 정상적인 상황에서 X축을 중심으로 한 회전을 제어하며, 다른 두 축과 서로 독립적입니다.

그러나 피치 각도가 ±90도에 도달할 때, 첫 번째 회전축(요축)과 세 번째 회전축(롤축)이 동일선상 또는 평행하게 되어 시스템이 하나의 회전 자유도를 잃고 오직 두 개의 자유도 회전만 실현할 수 있습니다. 이러한 현상을 김벌 락이라고 하며, 이는 오일러 각 표현법의 고유한 한계입니다.
|
김벌 락은 단순히 이론적 문제가 아니라, 실제 로봇 제어에서 로봇 말단 실행기가 특이 자세에 접근할 때 갑작스러운 대폭 회전이나 운동 불연속 현상이 나타날 수 있으며, 이는 정밀 조작에서는 허용되지 않습니다. |
쿼터니언
쿼터니언은 매우 효과적인 3차원 회전 표현 방법으로, 오일러 각의 특이성 문제를 극복할 수 있으며, q = w + xi + yj + zk로 쓸 수 있습니다. 여기서 w, x, y, z는 모두 실수 성분입니다. 회전에 사용될 때 쿼터니언은 "단위 놈"을 만족해야 하며, 즉 w² + x² + y² + z² = 1입니다.
장점:
-
오일러 각의 "김벌 락" 문제를 피할 수 있으며, 특이점이 없어 임의의 3차원 자세를 설명하는 데 적합합니다.
-
여러 회전을 합성할 때 쿼터니언 곱셈만 수행하면 되므로 효율이 높고 수치적으로 안정적입니다.
-
회전 보간 계산에 적합합니다. 구면 선형 보간(SLERP)은 두 쿼터니언 사이에서 부드러운 회전 경로를 생성할 수 있으며, 이는 로봇 궤적 계획에서 매우 유용합니다.
단점:
-
쿼터니언과 실제 3차원 회전 간의 관계를 직관적 기하학으로 이해하기 어려우며, 이해 문턱이 높습니다.
-
컴퓨터에서 쿼터니언으로 반복 변환을 수행할 때 수치 오차로 인해 쿼터니언이 더 이상 단위 쿼터니언이 아닐 수 있으므로 정기적인 정규화가 필요합니다.
-
쿼터니언에는 표현 중복성이 존재하며, q와 -q가 같은 회전을 나타내므로 일부 알고리즘에서 혼란을 야기할 수 있어 특별한 처리가 필요합니다.
회전 벡터
회전 벡터는 또 다른 간결한 3차원 회전 표현 방법으로, Rodrigues 회전 공식에 기반합니다. 모든 3차원 회전은 "특정 방향으로 얼마만큼 회전하는가"로 이해할 수 있습니다. 예를 들어 "x축을 중심으로 30도 회전", "[1,1,0] 방향으로 45도 회전"과 같습니다. 이 "방향"을 3차원 벡터(예: [1,0,0]은 x축 방향을 나타냄)로 표현하고, "회전 각도"를 하나의 수로 표현합니다. 둘을 곱하면 회전 벡터가 됩니다.
장점:
-
회전 벡터 표현 방식이 간결하여 소각도 회전을 설명하는 데 적합합니다.
-
회전 매트릭스와 쉽게 상호 변환할 수 있습니다.
단점:
-
회전 각도가 180도에 접근할 때 회전 벡터의 수치가 불안정해지며, 미세한 변화가 회전 결과에 큰 변화를 야기할 수 있어 구현 시 특별한 주의가 필요합니다.
-
오일러 각처럼 직관적이지 않고, 쿼터니언처럼 수치적으로 견고하지도 않습니다.
강체 변환
로봇공학에서 단순히 자세(회전)만 설명하는 것은 종종 부족하며, 동시에 위치(평행이동)도 설명해야 합니다. 강체 변환은 바로 이 문제를 해결하기 위해 제안된 통합 표현 방법입니다.
강체 변환은 물체가 3차원 공간에서의 회전과 이동(평행이동)을 의미하지만, 물체의 형태와 크기는 변경하지 않습니다. 보통 4×4 동차 행렬로 표현합니다:
[ R T ]
[ 0 1 ]여기서 R은 3×3 회전 매트릭스이고, T는 3×1 평행이동 벡터입니다. 이 4×4 행렬은 한 좌표계가 다른 좌표계에 대한 위치와 자세 관계를 완전하게 설명합니다.
동차 좌표의 도입으로 회전과 평행이동을 행렬 곱셈으로 통일하여 표현할 수 있습니다. 공간의 한 점 P에 대해, 새로운 좌표계에서의 좌표 P’는 간단한 행렬 곱셈으로 얻을 수 있습니다: P' = T × P, 여기서 P와 P' 모두 동차 좌표로 표현됩니다.
장점:
-
물체의 공간에서의 위치와 방향을 완전하게 설명할 수 있어 공간 운동의 통합 표현에 적합합니다.
-
행렬 곱셈을 통한 다중 변환의 직접적인 조합을 지원하여 로봇 운동학, 그래픽 변환 등에 적합합니다.
-
강체 변환 행렬은 우수한 수치 안정성을 가지고 있어 연속적인 변환 작업으로 인한 과도한 오차 누적이 발생하지 않습니다.
|